Finding the #MinimumRisk #portfolio on a two-security #EfficientFrontier

Posted by Elliot Noma on September 12, 2016 · Leave a Comment

frontier1

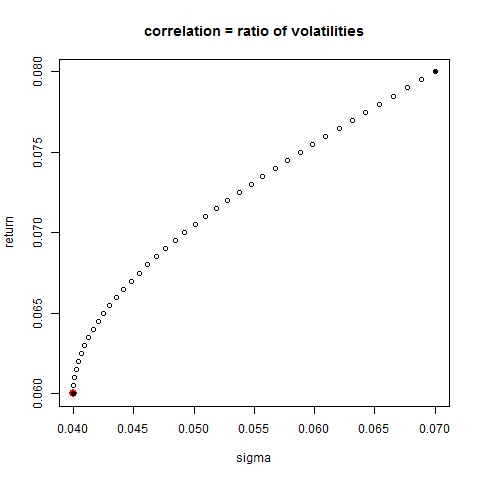
In the #Markowitz risk-return space, there is always a portfolio which #MinimizesVolatility. In recent years this allocation scheme has become increasingly popular as the risk free rate hovers near (or below) zero.

For a portfolio of two securities, there is an analytic solution which allocates capital to both securities to minimize the portfolio volatility. We minimize the variance of the portfolio (which is equivalent to minimizing the volatility) by finding the minimum for

$\sigma^2 = w^2 * \sigma_1^2 + (1-w)^2 * \sigma_2^2 + 2 * w * (1-w) * \rho * \sigma_1 * \sigma_2$

where w and (1-w) are the allocations, $\sigma_1$ and $\sigma_2$ are the volatilities of the two securities and $\rho$ is the correlation of the returns.

By solving for the first derivative with respect to w equal to zero,

$\frac{ \partial \sigma^2 } { \partial w } = 0$

we get

$w = \frac{ \rho * \sigma_1 * \sigma_2 - \sigma_2^2} { 2 * \rho * \sigma_1 * \sigma_2 - \sigma_1^2 - \sigma_2^2}$

We note the following

the returns of the securities do not enter into the allocations across the two securities
the higher the correlation, the greater the weight allocated to the lower-volatility security

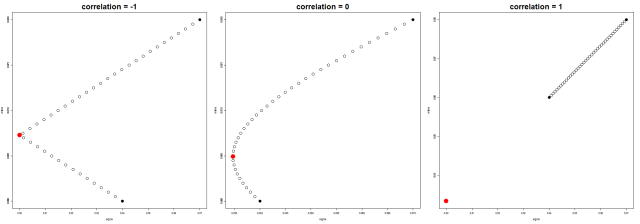
If we assume $\sigma_2$ > $\sigma_1$ , then we can consider the special cases where

$\rho = -1$

$w = \frac{ \sigma_2} { \sigma_2 + \sigma_1}$

$\rho = 0$

$w = \frac{ \sigma_2^2} { \sigma_2^2 + \sigma_1^2}$

$\rho = 1$

$w = \frac{ \sigma_2} { \sigma_2 - \sigma_1}$

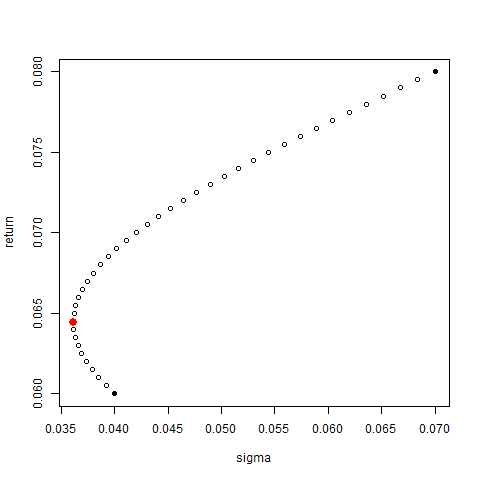
The less volatility security (#1) always receives the greater allocation. When the correlation is -1, the minimum volatility portfolio allocates to both securities. As the correlation increases, the allocation to the less volatile security increases.

extremefrontier

When $\sigma_1 = \rho * \sigma_2$ the less volatile security receives the full allocation. Higher values of $\rho$ create a portfolio with of a leveraged allocation to the less volatile security and a short position in the more volatile security.

frontier01weight

Filed under Financial Analysis, Position Sizing

Elliot Noma